CIVILIZACION INDIA
* El único documento
aC es el Sulva Sutra de Apastamba, anterior a la conquista de Alejandro Magno
(356-323 aC) buena parte del mismo se ha logrado situar hacia el s. VII aC
El Sulva Sutra es una especie de manual del constructor que
contiene reglas para erigir altares y variar sus dimensiones conservando su
forma. Su autor demuestra conocer el teorema de Pitágoras obtenido seguramente
de alguna manera empírica ya que no tiene demostración alguna, tampoco tienen
demostraciones las propiedades que anuncia, a las que no acompaña ninguna
figura, y cuando las hay no sirven de guía a un pensamiento mas o menos
riguroso, sino solo para poner ante el lector la prueba visual de la
legitimidad de la construcción.
* Sistema
posicional:
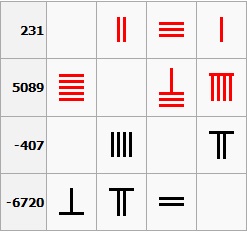
Tiene sus orígenes en la India, al principio los antiguos
Indios escribían los números mediante los símbolos del uno al nueve, y después,
con otro conjunto de símbolos para presentar las decenas, del diez al noventa.
Los múltiplos de cien, del mil, etc., se construían representando las unidades
multiplicadas por los símbolos para el cien, el mil… Esta notación se
simplificó más tarde, produciendo para la historia la notación posicional, que
no necesitaba más que los símbolos del cero al nueve. Hay controversia sobre la
fecha exacta de la transformación, pero la mayoría de las evidencias dan como
muy probables las cercanías del año 600. Sea como fuere en el 870 el sistema
posicional estaba ya establecido en la India se introdujo en Occidente a través
de sabios árabes y comerciantes asiáticos.
El sistema posicional se caracteriza por:
Una base decimal, una notación posicional y una forma
cifrada para cada uno de los 10 numerales basicos
Numeración alfabética india (izquierda) – transformación de
los números a través del tiempo (derecha)
* Multiplicación en
celdillas:
Para explicar el esquema en el que se basa, lo mejor es
recurrir a un par de ejemplos.
En el primero de ellos el número 456 aparece multiplicado
por 34; el multiplicando está escrito en la parte superior del retículo y el
multiplicador a la izquierda, y los productos parciales ocupan las celdas
cuadradas, de manera que al sumar los dígitos en diagonal de arriba a la
izquierda abajo a la derecha se obtiene el producto 15.504 que aparece en la
parte inferior y derecha del rectángulo.
En la figura 2 se da otro ejemplo para indicar que los datos se podían disponer también de otras maneras; aquí vemos el multiplicando 537 situado de nuevo en la parte superior y el multiplicador 24 en cambio a la derecha, mientras que el producto 12.888 se lee por la izquierda y la parte inferior del rectángulo.
* La división larga (método de la galera) :
Para ilustrar este método, supongamos la división de 44.977
por 382; en la figura 2.1 aparece hecha por el método moderno, y en la figura
2.2 por el método de la galera.
Este segundo se parece mucho al primero excepto en que el
dividendo aparece en el medio, ya que las restas se hacen cancelando los
dígitos y poniendo las diferencias encima de los minuendos y no debajo. Así
pues, el resto final 283 aparece en la parte superior derecha y no en la parte
inferior.
El proceso reproducido en la figura 2 es fácil de seguir si
tenemos en cuenta que los dígitos de un substraendo dado, como el 2674, o de
una diferencia dada, como la 2957, no figuran todos ellos necesariamente en la
misma fila, y que los substraendos aparecen escritos por debajo de la línea
central y las diferencias por encima; por otra parte, la posición en una
columna es importante, pero no la posición en una fila.
* El cero es un vacío. Es la ausencia de número y su origen,
es de origen Indio. En sánscrito el cero se dice sunya, que significa vacío o
en blanco. A Occidente llegó con mucho retraso y de mano de los árabes, que lo
tradujeron como sifr, de donde derivan los vocablos cifra y cero. En la India,
la utilización del cero estaba tan difundida en las costumbres, que este
aparece incluso en poemas y textos sagrados.
La concepción del cero es un logro de enorme importancia
cultural. No es fácil llegar a él.
* Números negativos en la India: Los indios no concebían las
matemáticas como geometría. Los matemáticos indios fueron los primeros en
reconocer las raíces negativas y las dos raíces cuadradas de un número
positivo. Además multiplicabas números positivos y negativos.
* Brahmagupta menciona dos valores de p, el <<valor
práctico>> 3 y el <<valor exacto>> raíz de 10 , pero no
menciona en cambio el valor más aproximado de Aryabhata, y en la trigonometría
que incluye su obra más conocida, el Brahmasphuta Siddhanta adopta como radio
del círculo el valor 3,270.
Brahmagupta calcula el <<área bruta>> de un
triángulo isósceles multiplicando la mitad de la base por uno de los lados
iguales; para el triángulo escaleno de base 14 y lados 13 y 15 calcula el
<<área bruta>>. Multiplicando la mitad de la base por la media
aritmética de los otros dos lados. En cambio, para hallar el área
<<exacta>> utiliza la fórmula de Arquímedes-Herón.
El resultado más bello en la obra de Brahmagupta es su
generalización de la fórmula de Herón para calcular el área de un
cuadrilátero: donde a, b, c y d son los
lados del cuadrilátero y s el semiperímetro. Este resultado queda un tanto
empañado pues sólo es válido para el caso de un cuadrilátero cíclico
(insciptible).
La fórmula correcta para un cuadrilátero arbitrario es , donde
es la semisuma de dos ángulos opuestos del cuadrilátero. También utiliza
expresiones que permiten obtener las diagonales de un cuadrilátero inscriptible
conocidos los lados, que hoy escribiríamos:
En su obra aparecen soluciones generales de ecuaciones
cuadráticas incluyendo las dos raíces incluso en los casos en que una de ellas
sea negativa; de hecho es la primera vez que aparece sistematizada la
aritmética de los números negativos y del cero.
Teorema de Brahmagupta
Para el resultado sobre el área de un cuadrilátero cíclico,
véase fórmula de Brahmagupta.
En geometría euclidiana, el teorema de Brahmagupta (llamado
así en honor al matemático indio Brahmagupta) da una condición necesaria sobre
laperpendicularidad de las diagonales de un cuadrilátero cíclico (inscriptible
en un círculo).
Enunciado
Si las diagonales de un cuadrilátero cíclico son
perpendiculares, entonces toda recta perpendicular a un lado cualquiera del
cuadrilátero y que pase por la intersección de las diagonales, divide al lado
opuesto en dos partes iguales.
(BD) ┴ (AC) y (EF) ┴ (BC) implica AF = FD
|
Construcción y demostración
Dado un cuadrilátero inscriptible ABCD cuyas diagonales son
perpendiculares, se quiere demostrar que AF =FD. Para ello, se demostrará que
AF y FD son ambos iguales a FM.
Los ángulos FAM y CBM son iguales (debido al teorema de los
ángulos inscritos que intersecan al mismo arco de círculo). Además, los ángulos
CBM y CME son ángulos complementarios al ángulo BCM. Finalmente, AFMes un
triángulo isósceles, y por consecuencia, sus lados AF y FM son iguales.
De manera análoga se demuestra que FD = FM. Los ángulos FDM,
BCM, BME y DMF son todos iguales, luegoDFM es un triángulo isósceles, de donde
FD = FM. Se sigue que AF = FD, lo que demuestra el teorema.
* En esta obra él definió el cero como el resultado de
restar un número de sí mismo. Él dio algunas propiedades:
1) Cuando el cero se suma a un número o se resta de un
número, el número permanece inalterado.
2) Un número multiplicado por cero es cero.
Él también da reglas aritméticas en términos de fortunas
(números positivos) y deudas (números negativos):
1) Una deuda menos el cero es una deuda.
2) Una fortuna menos el cero es una fortuna.
3) Una deuda restada del cero es una fortuna.
4) Una fortuna restada del cero es una deuda.
5) El producto de cero multiplicado por una deuda o fortuna
es cero.
6) El producto o cociente de dos fortunas es una fortuna.
7) El producto o cociente de dos deudas es una fortuna.
8) El producto o cociente de una deuda y una fortuna es una
deuda
9) El producto o cociente de una fortuna y una deuda es una
deuda.
Bramahgupta intentó extender la aritmética para incluir la
división por cero, entonces:
1) Cero dividido por cero es cero.
2) Cero dividido por negativo o los números positivos son o
cero o se expresa como una fracción con cero como numerador y la cantidad
finita como denominador. Realmente, Brahmagupta está diciendo que n dividido
por cero es n/0. Él se equivoca cuando dice que cero dividido por cero es cero.
Sin embargo es un esfuerzo inteligente de Brahmagupta por extender la
aritmética.
* Bhaskara se
enfrentó a el problema de la división por cero. Afirmó que (a/0).0=a. la
primera vez que nos encontramos con la afirmación de que a/0=0 es en el vijaganita de bhaskara.
* Los indios
estudiaron con profundidad la trigonometría, sobre todo por su utilidad para
hacer cálculos astronómicos, aunque también para aplicarla en ecuaciones
indeterminadas, el algebra y la combinatoria. De hecho, el concepto y la
palabra seno proviene de un tratado de astronomía del siglo V, el
Paitamahasiddhanta. La otra consistió en la introducción de lo equivalente a la
función seno en trigonometría, para reemplazar las tablas de cuerdas griegas;
las tablas más antiguas de la relación seno que han llegado hasta nosotros son
las que figuran en los Siddhantas y en el Aryabhatiya, donde se dan los senos
de los ángulos menores o iguales que 90°para 24 intervalos angulares iguales de
3(3° 4/ ) cada uno. Para expresar la longitud del arco y la del seno en
términos de la misma unidad, se tomaba como radio 3.438 unidades y la
circunferencia correspondiente como 360 · 60 = 21.600 unidades; estos valores
implican un valor de π que coincide con el de Ptolomeo hasta la cuarta cifra
significativa, pero Aryabhata utiliza en otros contextos el valor 10 para π,
valor que aparece tan frecuentemente en la India que se le conoce a veces como
<<el valor hindú>> de π.
* La relación entre
la circunferencia y su diámetro:
“Sumar 4 a 100 multiplicar por 8, sumar todavía 62000 se
obtiene así un valor aproximado (asanna) de la circunferencia de un circulo
cuyo diámetro es de 2 miríadas”.
Este verso de Aryabhata (matemático y astrónomo indio) del
siglo IV nos da la más antigua formulación sobre el valor aproximado de la
relación que más adelante se denominara pi.
Un ióyana es una unidad de medida utilizada en la antigua
India. Los estudiosos de la actualidad estiman que mediría 6,2 km
aproximadamente. Existe una medida, el majá-ióyana, que mide 1000 ióyanas.
