- Signos gráficos
- Kaishu:
- Lishu:
- Cantidades numéricas
La actual numeración oral china presenta unas características que la
hacen distinta de la occidental. En efecto, las palabras asignadas a las diez
primeras cifras son:
- Sistema de numeración
Las varillas de numeración fueron utilizadas por los antiguos Chinos
durante más de 2.000 años. Tras la aparición del ábaco,
se abandonó el uso de las varillas de contar excepto en Japón,
donde de la numeración con varillas se desarrolló una notación simbólica para
el álgebra.
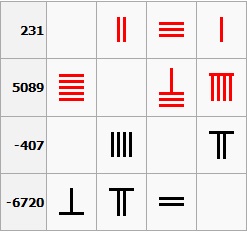
Las varillas de contar representan una unidad por varilla y cinco para
la varilla puesta de forma perpendicular. Para evitar confusiones, se emplean
formas verticales y horizontales de forma alterna. En general, se emplean
varillas verticales para las posiciones de las unidades, centenas, miríadas,
etc., mientras que las horizontales se emplean para las decenas, los millares,
los centenares de millar, etc. Los antiguos chinos entendían claramente el
concepto de los números negativos y del cero, aunque no tenían
símbolo para este y en su lugar dejaban un espacio en blanco.
Ejemplos:
A partir de las varillas de contar se ha formado un sistema de numeración posicional en
que las cifras son agrupaciones de varillas. Los números positivos se escriben
como se ha explicado antes y los negativos se escriben tachando el último
dígito con una barra diagonal (no aceptaron la idea de que un número
negativo pudiera ser una solución de una ecuación). La barra vertical para las formas horizontales de los números del 6 al 9
se escribe más corta para que cada carácter tenga la misma altura.
El cero queda representado por un círculo (〇).
- Operaciones aritméticas
- Suma y resta con varillas
Supongamos que hemos de realizar la suma: 378 +
296
- En
primer lugar, se colocan como actualmente uno sobre el otro de manera que
coincidan las unidades del mismo orden (unidades con unidades, decenas con
decenas, etc.).
3
7 8
2 9
6
- A
continuación se comienza la suma por las unidades más altas, en este caso las
centenas. El resultado así de sumar 3 y 2 centenas (5) sustituye a las centenas
del sumando superior desapareciendo las del inferior por haber sido realizado.
5
7 8
9
6
- Seguidamente,
se suman las decenas (7 y 9) pero como el resultado excede a diez, la centena
que resulta se añade a las 5 que se tenían como resultado.
6
6 8
6
- Que da
paso a 674 como resultado final.
El sucesivo “borrado” de cifras del primer sumando para ser sustituidas por las del resultado final y la desaparición de cifras del segundo sumando ya operadas debían dar lugar a un manejo rápido de las varillas que consistiría en disponerlas de modos diferentes para expresar las distintas cifras.
La operación de sustracción tiene la misma
disposición que la de la suma, como se ha inferido a partir del estudio de la
división, donde han de realizarse sistemáticamente. La disposición de las
cantidades es igual y el comienzo de las operaciones parciales también comienza
por las unidades más altas. Cuando no es posible realizar la resta porque la
cifra del minuendo es menor que la correspondiente del sustraendo, se detrae
una unidad del orden superior del minuendo.
Así, en el caso de restar 536 – 389 los pasos a
realizar serían los siguientes:
5 3
6
3 8
9
- Primero
se restan las centenas:
2
3 6
8 9
- Luego
las decenas, tomando una centena del resultado que ha quedado en el minuendo o
bien realizando directamente 23 – 8:
1 5 6
9
- Para
terminar con las unidades del mismo modo:
1 4 7
- Multiplicación
Supongamos
que hemos de multiplicar 346 x 8. Se disponen el multiplicando (shang) sobre el
multiplicador (xia) de manera que la cifra de las unidades de éste (en este
caso no hay más que unidades) se coloque bajo la unidad superior del
multiplicando:
3 4 6
8
Entonces
se multiplica 8 x 3, la cifra colocada encima, de manera que el resultado se
disponga en medio como resultado parcial (zhong).
3
4 6
2 4
8
2 4
8
Hecho esto, desaparece la cifra del multiplicando ya operada (3 centenas) y el
multiplicador (8) se traslada un lugar a la derecha para operar ahora las
decenas del primero.
4 6
2 4
8
2 4
8
Realizada
esta operación (8 x 4 = 32) el resultado se añade a la cantidad intermedia:
6
2 7 2
8
2 7 2
8
Tras el
consabido traslado a la derecha del multiplicador, se realiza la última
multiplicación parcial (6 x 8 = 48) procediéndose del mismo modo y
desapareciendo el multiplicando y multiplicador.
2 7 6 8
- División
“Primero,
colocar 6561 en posición intermedia por ser el dividendo. Debajo, colocar 9
personas como el divisor”.
6
5 6 1
9
9
“En la
posición superior colocar 700”
7
6 5 6 1
9
6 5 6 1
9
“El 7 superior llama al 9 inferior; 7 veces 9
son 63, lo que significa quitar 6300 de la posición intermedia”.
7
2 6 1
9
2 6 1
9
“Mover el número de la posición inferior un
lugar y entonces colocar 20 en la posición superior”.
7
2
2 6 1
9
2 6 1
9
“El
2 superior llama al 9 inferior; 2 veces 9 son 18, lo que significa quitar 180
de la posición intermedia”.
7
2
8 1
9
8 1
9
“De
nuevo, mover el número en la posición inferior un lugar y entonces colocar 9 en
la posición superior”.
7
2 9
8 1
9
9
“El 9
superior llama al 9 inferior; 9 veces 9 son 81, que significa quitar 81 de la
posición intermedia. Ésta queda entonces vacía”.
7
2 9
9
“Desechar
el número en la posición inferior. El resultado en la posición superior es lo
que cada persona recibe”.
7 2 9
- Unidades de medida
Unidades utilizadas en torno al peso de los productos y materias primas:
1 shi = 4 jun
1 jun = 30 jin
1 jin
= 16 liang
1 liang = 24 zhu
donde
la unidad más alta, el shi, equivalía a unos 29,5 kg actuales.
En la
agricultura se manejaban sobre todo medidas de volúmenes de granos y líquidos,
cuyas unidades más frecuentes eran las siguientes:
de
forma que:
1 shi = 10 dou
1 dou = 10 sheng
1 dou = 10 sheng
Relaciones métricas de las unidades de longitud:
de forma que
1
li = 180 zhang
1 zhang = 10 chi
1 bu = 6 chi
1 chi = 10 cun
1 zhang = 10 chi
1 bu = 6 chi
1 chi = 10 cun
- Notación de Fracción
Los
chinos conocían bien las operaciones con fracciones ordinarias, hasta el punto
de que en este contexto hallaban el mínimo común denominador de varias
fracciones. Al igual que hacían en otras materias, también aquí establecían
analogías con los distintos sexos, refiriéndose al numerador como "el
hijo" y al denominador como "la madre"; el énfasis generalizado
en toda la cultura china sobre los principios del yin y el yang hacia más fácil
seguir las reglas para manipular fracciones. Más importante que estas
curiosidades era, no obstante, la tendencia a la decimalización de las
fracciones en China. La adopción de un sistema decimal en pesos y medidas dio
como resultado que se impusiera el hábito decimal en el manejo de las
fracciones, que puede rastrearse, según se dice, tan lejos en el tiempo como el
siglo XIV a.C. Algunas veces se adoptaron ciertas artimañas de carácter decimal
para aligerar un poco la manipulación de las fracciones; así, por ejemplo, en
un comentario a los nueve capítulos que data del primer siglo de nuestra era,
nos encontramos con el uso de unas reglas que hoy nos son muy conocidas para el
cálculo de raíces cuadradas y cubicas, equivalentes a escribir:
, y que facilitan la decimalización al hacer extracciones de raíces.
No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.